前言

在昨日的內容中我們學習到了深度學習、機器學習和人工智慧之間的差異，讓我們對這些概念有了初步的理解。今天我們將進一步深入深度學習的領域，並介紹其中最基礎、也是最簡單的模型架構單層感知器(Single Layer Perceptron)

而我們在接下來的幾天裡，將會透過這個模型，先清楚地了解深度學習如何通過複雜的計算過程，從輸入數據中生成預測結果，並通過這些預測結果來修正模型的錯誤計算，以提高預測的準確性。最後我們將通過程式碼實作的方式把這些數學式轉換成對應的程式碼。這樣你能對深度學習的內部運作有更直觀的認識，並打下紮實的基礎，以便在未來進一步探索和應用更高階的深度學習技術。

單層感知器(Single Layer Perceptron)

單層感知器是神經網路的最簡單形式之一，它最早由 Frank Rosenblatt 在 1958 年提出。單層感知器是一種二元分類器，主要用來解決線性可分的問題。它能夠根據輸入特徵來預測輸出是否屬於某一類別。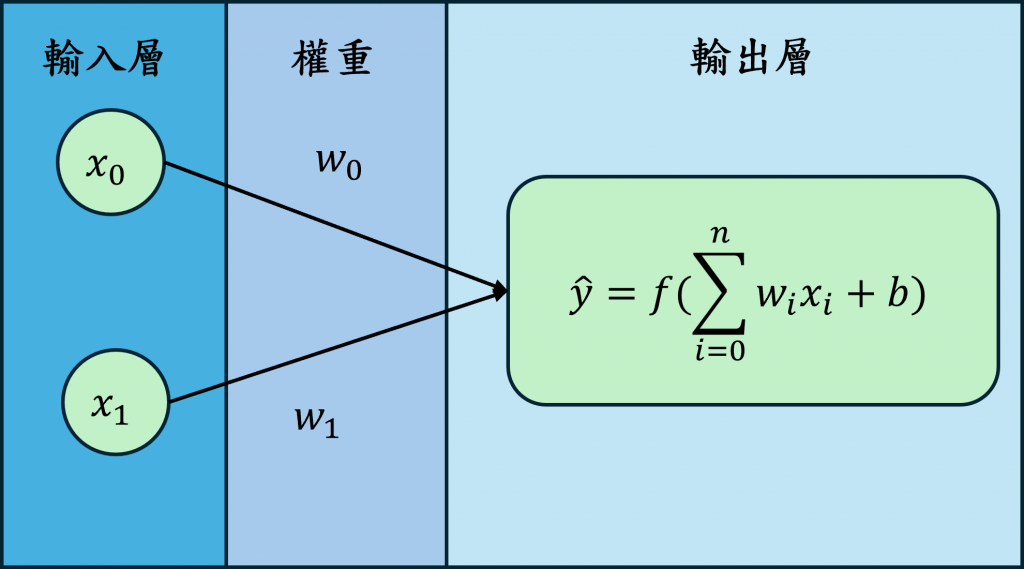

單層感知器由輸入層（Input Layer）、權重（Weights）、輸出層（Output Layer）三個部分組成，輸入層將資料以向量(Vector)的形式輸入，每個輸入對應一個特徵(Feature)，而每個輸入特徵都會有一個權重值(Weights)，這些權重會與輸入相乘，最後經過輸出層將輸入特徵與權重相乘的結果加總，然後通過一個激勵函數(Activation Function)來決定輸出的類別，其數學表達式如下: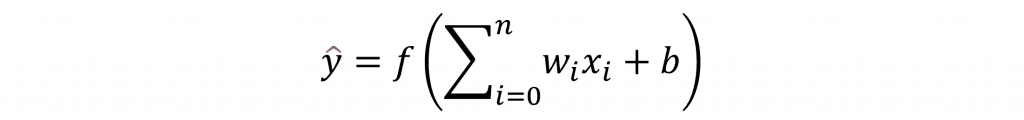

其中f(x)在單層感知器中會使用的是階梯函數(Step Function)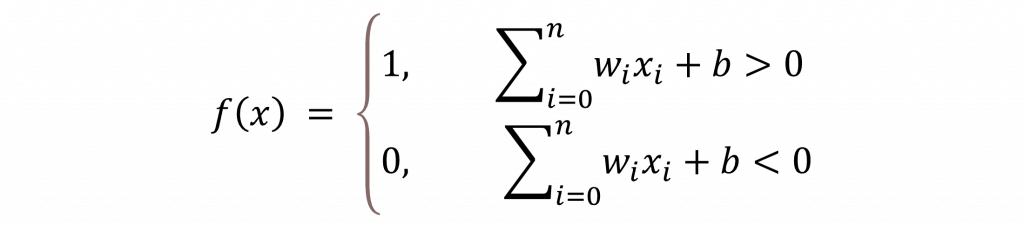

該函數的用法是將計算結果大於 0 的轉換成 1，小於 0 的結果轉換成 0，這樣就能完成一個簡單的二元分類器。而這種通過模型計算出答案的過程在深度學習中被稱之為前向傳播(Forward Propagation)

偏移量 b 可能為 0，其參數代表答案的偏向。例如，當我們知道答案可能會偏向於正值時，偏移量可以設定為大於 0 的常數；若答案可能為負值，偏移量則可以設定為小於 0 的常數。

不過由於權重是隨機初始化的狀態，因此在模型的初始狀態基本上運算出的答案都是錯誤的，因此我們需要有一個有效的方式來調整其權重的變化，而這個動作就叫做反向傳播(Backward Propagation)，其基本概念就是通過計算出預測標籤與實際標籤的損失值(Loss)，並計算出會變動的參數(Parameter)的梯度(Gradient)，以找出這些參數的變化方向。

上述公式中，我們可以發現輸入 x 並不會改變，且偏移量 b 是常數，因此我們應該調整適當的權重 w 來計算出正確的答案。因此我們需要計算出損失值對於權重的變化量 𝜕Loss/𝜕w。在這裡我們先假設損失函數 (Loss Function) 是使用均方誤差 (Mean-Square Error, MSE)，其數學式如下: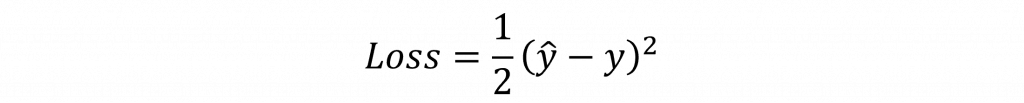

接下來我們需要針對這個損失函數對w進行偏微分的動作，以計算出損失值對於權重的變化量 𝜕Loss/𝜕w，不過由於階梯函數是一種不連續的函數，因此我們可以忽略其計算結果，直接使用wx+b的運算結果進行處理即可，這時我們將能夠使用連鎖律(Chain rule)推理出以下結果。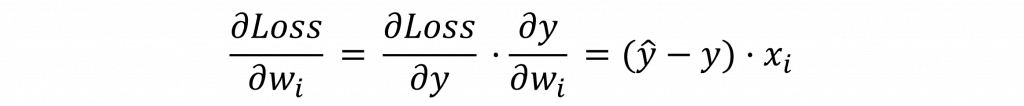

而計算完的結果將代表者每個權重的變化量與變化方向，我們可以將權重、損失值與梯度整理成下圖之間的關係。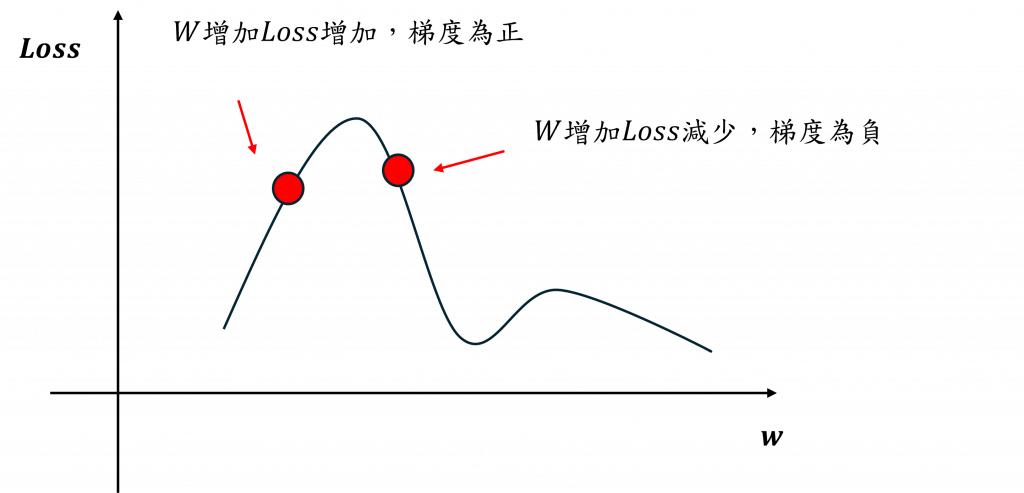

在我們的最終目的就是計算出 𝜕Loss/𝜕w = 0，這也代表著在上圖中我們會想要讓右邊的紅點向右移，左邊的紅點向左移，因此對其優化方是我們可以採用梯度下降法(Gradient descent)，其數學式如下：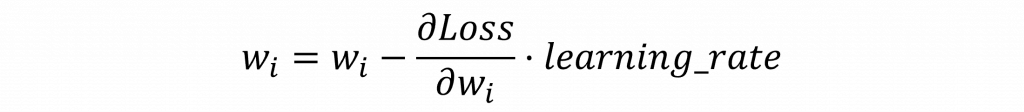

其中我們可以發現，在調整權重時還會與學習率(Learning rate)進行運算。學習率通常是一個非常小的數值，原因是如果我們計算出來的梯度太大，圖中的紅點就會一次移動得很遠。因此通過這個學習率超參數，我們可以控制紅點的移動速度，使其逐漸收斂到損失值較低的位置。而這種優化的算法在深度學習中則被稱之為優化器(Optimizer)

總結

這次我們學習了深度學習中監督式學習的完整流程，並解析了其中的數學原理。你可能會覺得今天的內容有些複雜，因此在今天的最後，我會用一句話來總結我們今天學到的內容。其實整個深度學習的過程就是前向傳播計算答案、損失函數計算損失值、反向傳播計算梯度、使用梯度配合優化器更新可調參數，通過不斷迭代最終計算出答案。這樣子理解整個深度學習的概念就變得簡單許多了!